Условный оператор
Если в программе необходимо выполнять те или другие действия в зависимости от выполнения (или невыполнения) некоторых условий, то необходимо использовать условный оператор (иногда он называется оператор ветвления). В общем виде он записывается так:
if
<условие>
then
<серия
операторов 1> else
<серия
операторов 2>
Помните, что в формате оператора служебные слова (if,
then,
else
)
пишутся ровно также, а содержимое стрельчатых скобок заменяется (включая
сами скобки) конкретными операторами с соблюдением правил.
Выполняется условный оператор следующим
образом: если условие истинно, то выполняется серия операторов, описанных после
служебного слова
then,
если ложно - серия
операторов, описанных после после служебного слова
else
.
Наверняка Вы встречались с алгоритмами, в которых необходимо было выполнить
некоторые действия в случае истинности условия, а в случае ложности - нет. В
языке программирования в этом случае применяется неполная форма условного
оператора:
if <условие> then <серия операторов 1>
При этом, если условие ложно, то программа выполняет операторы, следующие за данным if .
Рассмотрим употребление
условного оператора на примерах.
Пример 1.
Определить четность значения целой переменной к.
if k mod 2=0 then writeln( k, 'чётное') else writeln( k, 'нечётное')
Пример 2.
Распечатать число n, если оно делится на 7.
n:=127
if n mod 7=0 then writeln( 'n=', n)
Понятно, что при программа не напечатает значение переменной n.
Если серии операторов состоят более, чем из одного оператора, то операторы группы (серии) записываются списком с разделителем " ; " и заключаются в блоковые скобки begin end.
Пример 3.
Если квадратное уравнение имеет корни, то вычислить и напечатать их, в противном случае выдать сообщение "корней нет".
d:=b*b-4*a*c;
if d>0 then begin x1:=(-b-sqrt(d))/(2*a); x2:=(-b+sqrt(d))/(2*a); writeln( 'x1='x1; x1; 'x2='; x2) end else writeln( 'решений нет')
Условие чаще всего содержат операцию отношения
| Математическое отношение двух величин | Запись отношения на языке | Комментарий | Примеры |
| A = B | A = B | A равно В | Y = X + 2 |
| A ≤ B | A <= B | А меньше или равно В | SIN(2*X) <= 0 |
| A < B | A < B | А меньше В | A*A + B*B < C + 5 |
| A ≥ B | A >= B | А больше или равно В | tan(AL) + tan(AL/2) >= 2 |
| A B | A > B | А больше В | 1/X > 1/(X*X) |
| A ≠ B | A >< B | А не равно В | 5*X*X+3≠ 8*X |
Общий вид отношения: <Выражение 1> <Операция отношения> <Выражение 2>
Выражение - совокупность переменных, функций и констант, соединённых знаками математических операций.
Для того, чтобы определить истинность условия, необходимо вычислить значение выражений и понять, справедливо ли соотношение их соединяющее. Понятно, что к моменту вычисления истинности условия необходимо, чтобы значения всех входящих в него переменных должны быть определены. В примере 3 к моменту выполнения оператора if переменные a, b, с должны быть определены и значение переменной d должно быть вычислено.
Если проверяемые условия сложные или их много, можно применить специальные приёмы, в которых каждое простое условие вычисляется отдельно (истинно - логическая "1", ложно - логический "0"), а затем анализировать сумму логических "единиц".
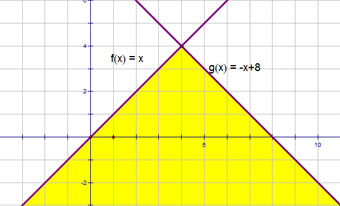
Пример 4.

Определить принадлежит ли точка с координатами (x; y) закрашенной части области.
p:=0;
if
y < x
then
p:=p+1;
if y
< -x+8
then
p:=p+1;
if
p=2
then
writeln( 'принадлежит')
else
writeln( 'не
принадлежит'')
Если мы научимся составлять и определять истинность сложных условий, то наше программирование будет гораздо изящней и эффективней.
Забегая чуть вперёд, покажем на этом примере возможность использования логической связки для проверки сложного условия
if y<x and y<-x+8 then writeln( 'принадлежит') else writeln( 'не принадлежит'')
Подчёркнутое слово это логическая связка " и" , которая строит сложное логическое условие из двух простых.
Логический тип данных.
Надеемся, что после приведённых примеров стало понятно как работает оператор if. Внимательному читателю, наверное, понятно, что про условие на момент работы условного оператора можно однозначно сказать истинно оно или ложно. Понятно, что должны существовать правила вычисления истинности или ложности сложного условия в зависимости от логических значений простых условий и логических связок.
Теперь настал момент изучить эти правила и научиться их применять. Поэтому мы немного окунёмся в мир математической логики, для более глубокого изучения её законов мы обратимся к соответствующим страницам нашего сайта.
Логика оперирует высказываниями. Этим термином мы будем пользоваться наравне с термином "условие". Высказывание - это любое повествовательное предложение, относительно которого можно сказать истинно оно или ложно. Объект алгебры логики принимает одно из двух значений: истина ("1", true) или ложь ("0", false). Высказывание, составленное из простых с помощью логических связок (операций), называется сложным. В этом разделе мы определим три основные логические операции.
| Логическая операция | Обозначение | Определение | Аналогия с теорией множеств | |
| Логическое умножение Операция "И" (конъюнкция) | A·B
AB A и B
A˄B A&B A and B |
Сложное конъюнктивное высказывание истинно тогда и только тогда, когда истинно каждое его составляющее. |
 |
Элемент принадлежит пересечению множеств (коричневая область), если он принадлежит каждому множеству красной области, зелёной области, жёлтой области). |
| Логическое сложение Операция "ИЛИ" (дизъюнкция) | A+B A или B A˅B A or B | Сложное дизъюнктивное высказывание истинно тогда и только тогда, когда истинно хотя бы одно его составляющее. |

|
Элемент принадлежит объединению множеств (цветная область), если он принадлежит хотя бы одному множеству (оранжевой области, зелёной области, голубой области). |
| Логическое отрицание Операция "НЕ" | не А not A A ¬A | Если высказывание истинно, то его отрицание ложно и наоборот. | 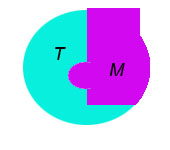 |
Элемент принадлежит множеству M, если не принадлежит множеству Т - его дополнению и наоборот. |
Составим таблицу истинности для логических операций исходя из их
определения; будем обозначать истинность как "1", ложь - как "0".
Для начала операции логического сложения и логического умножения будем
производить с двумя высказываниями.
| А | В | A˄B | A˅B | A |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 |
Порядок выполнения операций: отрицание, конъюнкция, дизъюнкция. Изменять порядок можно с помощью скобок.
Пример 5.
По введенной паре координат определить, принадлежит ли точка окрашенной области.
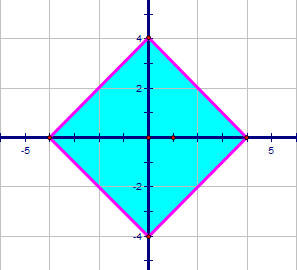
Границы ромба задаются отрезками, лежащих на прямых, уравнения которых
можно записать.
Чтобы точка лежала внутри ромба, необходимо, чтобы выполнялось одновременно
четыре условия:
1) точка лежит ниже прямой, проходящей через точки точки (0; 4) и (-4; 0)
2) точка лежит ниже прямой, проходящей через точки точки (0; 4) и (4; 0)
3) точка лежит выще прямой, проходящей через точки точки (0; -4) и (4; 0)
4) точка лежит выше прямой, проходящей через точки точки (0; -4) и (-4; 0)
Как записать уравнение прямой, проходящей через точки (х1; у1) и (х2; у2)
у=кх+в, где к=(у1-у2)/(х1-х2), в=у1-кх1
1) у=х+4
2) у=-х+4
3) у=х-4
4) у=-х-4
Для решения задачи мы могли бы написать сложное условие: (у<x+4)
and (y<-x+4) and (y>x-4) and (y>-x-4) и это было бы правильно, но
поскольку ученик старшего класса заметит некоторую симметрию в формулах линейных
функций, то это может выглядеть компактней, а именно:
|х|+|y|≤4, а на языке программирования нам надо использовать встроенную функцию abs - вычисление модуля.
Наш условный оператор выглядит так:
if abs(x)
+ abs(y) ≤ 4
then
writeln( 'точка
принадлежит
ромбу') else
writeln( 'точка
лежит вне ромба'')